02011 复变函数论
江苏教育学院编 (高纲号 0810)
一、复数与复变函数
一、要求
(一)明确复数、区域、复平面、扩充复平面,逐段光滑曲线等概念。
(二)明确复变函数概念和几何意义,掌握一些简单函数的变换性质。
(三)掌握复变函数的极限和连续性的概念和基本性质。
(四)熟练掌握复数的有关计算,会作点集的图形。
二、考试内容
(一)复数概念、复数的表示法及其代数运算、复数的模与幅角、共轭复数及其简单运算。
(二)平面点集基本概念,曲线(连续曲线、约当曲线、逐段光滑曲线)、区域(单连通区域、复连通区域)、复平面。
(三)复变函数的概念及其几何意义,复变函数的极限与连续性。
(四)无穷远点,扩充复平面。
二、解析函数
一、要求
(一)掌握导数、解析函数的概念。
(二)掌握C——R条件,并能熟练地判断复变函数的可导性和解析性。
(三)掌握复基本初等函数的定义和基本性质。
(四)掌握正整幂函数、根式函数、指数函数、对数函数的变换性质,了解根式函数单值解析分支的取法。
二、考试内容
(一)导数、解析函数、C--R条件。
(二)初等函数:正整幂函数与根式函数,指数函数与对数函数,三解函数与反三角函数,双曲函数,一般幂函数和一般指数函数。
三、复变函数的积分
一、要求
(一)明确复积分的概念及其基本性质。
(二)会证柯西积分定理和柯西积分公式;理解解析函数的无限可微性和莫勒拉定理。
(三)熟练地掌握复积分的计算方法。
(四)理解刘维尔定理,会证代数基本定理。
(五)掌握解析函数与调和函数的关系。
二、考试内容
(一)复积分的概念、基本性质及其计算方法。
(二)柯西积分定理(在f'(z)连续的条件下,用格林公式证明)。不定积分,复连通区域上的柯西积分定理。
(三)柯西积分公式,解析函数的无限可微性。
(四)柯西不等式、刘维尔定理、代数基本定理。
(五)莫勒拉定理。
(六)解析函数与调和函数的关系。
四、解析函数的幂级数表示法
一、要求
(一)明确收敛、绝对收敛、一致收敛、内闭一致收敛、幂级数、收敛半径、收敛圆、泰勒级数等概念。
(二)了解一致收敛的函数项极数的分析性质。
(三)掌握解析函数的零点孤立性定理和唯一性定理,了解最大模原理的含义。
(四)会求幂级数的收敛半径,了解幂级数的和函数在收敛圆周上必有奇点。
(五)会求简单初等函数的泰勒展开式。
二、考试内容
(一)复数项极数、收敛、绝对收敛。
(二)复变函数项级数、收敛、一致收敛、内闭一致收敛、一致收敛的函数项级数的分析性质。
(三)幂级数、阿贝尔定理、收敛半径、收敛圆、幂级数和函数的解析性。
(四)泰勒定理。基本初等函数的泰勒展开式。
(五)解析函数零点的孤立性、唯一性定理,最大模原理。
五、罗朗级数、孤立奇点
一、要求
(一)明确罗朗级数、孤立奇点、可去奇点、极点、本性奇点等概念。
(二)会求简单函数的罗朗展式。
(三)会判别孤立奇点的类型。
二、考试内容
(一)解析函数的罗朗展式。
(二)解析函数的孤立奇点的概念、分类以及函数在孤立奇点领域内的性质。
(三)解析函数在无穷远点的性质。
六、残数及其应用
一、要求
(一)掌握残数概念和残数的求法。
(二)掌握残数定理的证法并会用残数定理计算曲线积分。
(三)会用残数理论计算定积分和广义积分(三种类型);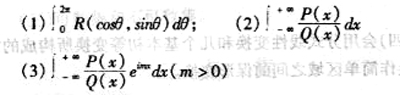
(四)了解幅角原理、儒歇定理,会用儒歇定理判断某些方程在指定区域内根的个数。
二、考试内容
(一)残数定义、残数求法、有限复平面上的残数定理。
(二)解析函数在无穷远点上的残数、扩充复平面上的残数定理。
(三)用残数计算曲线积分。
(四)用残数计算一些定积分和广义积分。
(五)儒歇定理及其应用。
七、保形变换
一、要求
(四)会用分式线性变换和几个基本初等变换所构成的复合变换作简单区域之间的保形变换。 二、考试内容 (一)导数的模和幅角的几何意义,保角变换,保形变换。 (二)解析变换的保域性(不证),单叶解析变换的保形性。 (三)分式线性变换用其分解,分式线性变换的性质及几个典型的分式线性变换。 (四)简单复合变换。
(一)掌握导数的模和幅角的几何意义。
(二)明确保角变换和保形变换的概念。了解解析变换的保域性。掌握单叶角析变换的保形性。
(三)掌握分式线性变换的性质和几个典型的分式线性变换。
选用教材意见
《复变函数论》 钟玉泉编 高等教育出版社出版